Bruce A Reznick
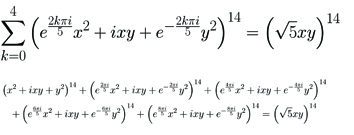 Sums of Powers of Polynomials
Sums of Powers of Polynomials
Mathematicians have long been fascinated by polynomial identities: equations that hold for all choices of variable. Polynomial identities often seem mysterious, coming from “nowhere” and requiring no additional hypotheses. They can reflect deep mathematical phenomena. During his Center appointment Professor Reznick plans to construct new identities, especially as sums of squares (or higher powers) of polynomials, and determine their additional implications.
In 1900, David Hilbert identified twenty-three outstanding mathematical problems for the next century. The 17th asked whether a polynomial p that takes only non-negative values must be expressible as a sum of squares of quotients of polynomials. Although this problem was solved in the 1920s (the answer is yes), the solution is non-constructive. Professor Reznick and his collaborators have worked for thirty years on constructive solutions. In applied mathematics, such constructive solutions to the 17th Problem provide “certificates” that given inequalities hold.
Professor Reznick’s “universal denominator” theorem for Hilbert’s 17th Problem uses so-called Hilbert Identities, which are also important in number theory, combinatorics, functional analysis, numerical analysis, and computational real algebraic geometry. For example, Hilbert Identities can specify how to disperse a set of points evenly on the surface of a sphere. A different kind of identity was found by François Viète in 1591. Reznick has shown that Viète’s identity is a special case of a basic operation in elliptic curve theory, not worked out until centuries later. This interpretation has led to a deeper understanding of elliptic surfaces, a subject of importance in certain encryption schemes.
