Nathan Dunfield
 The Linkage Between Topology and Geometry in Dimension 3
The Linkage Between Topology and Geometry in Dimension 3
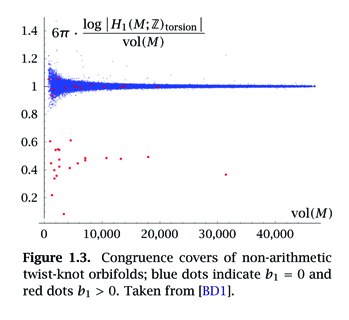
In topology, a 2-manifold is an object that looks locally like a plane, for example a sphere or the surface of a doughnut. This research project studies 3-manifolds, which are objects that look locally like the ordinary 3-dimensional space we live in but whose global structure may be twisted up in complicated ways. Starting in the late 1970s, W. Thurston revolutionized the field by discovering that many 3-manifolds have homogeneous geometries, which include the round geometry of a 3-dimensional sphere, and that one can study the topology of a 3-manifold via this geometry. This profusion of geometry was confirmed by Grigori Perelman’s stunning proof of Thurston’s Geometrization Conjecture in the early 2000s. While this geometric perspective has been central to the solution of many long-standing problems, there are many facets of the theory where the precise relationship between different topological and geometric features of the same 3-manifold remains obscure. This project aims to better understand these relationships in the context of torsion growth in towers of covers of hyperbolic 3-manifolds, a question in part motivated by deep questions in number theory and geometric analysis.
