Marius Junge
 Interaction Between Quantum Information Theory and Operator Space Theory
Interaction Between Quantum Information Theory and Operator Space Theory
In quantum information theory, quantum mechanics is used to submit information faster or more efficiently than via classical tools. On the theoretical side, quantum algorithms are predicted to be significantly faster in factoring numbers into prime factors than their classical counterparts. This area of specialization has an outstanding tradition at the University of Illinois, including work by CAS Professor Anthony Leggett (Nobel Prize in Physics, 2003) and Professor Paul Kwiat.
A number of experiments and computations show that in quantum mechanics certain phenomena can occur that cannot be explained using a classical model or using local hidden variables. The inequalities used to show nonlocality are called Bell inequalities. A violation of Bell inequalities then turns out to be a good thing: more information can be transmitted with quantum tools than with classical tools.
Professor Junge wants to know how much better the quantum setting is compared to the classical one by finding Bell inequalities with a large violation. The connection between this question and his core research in operator space theory was discovered through lucky circumstances involving a Ph.D. defense in Spain. The outcome is a proof that for a system with three parties and with a linear method of detection one can have arbitrary large violation in Bell inequalities.
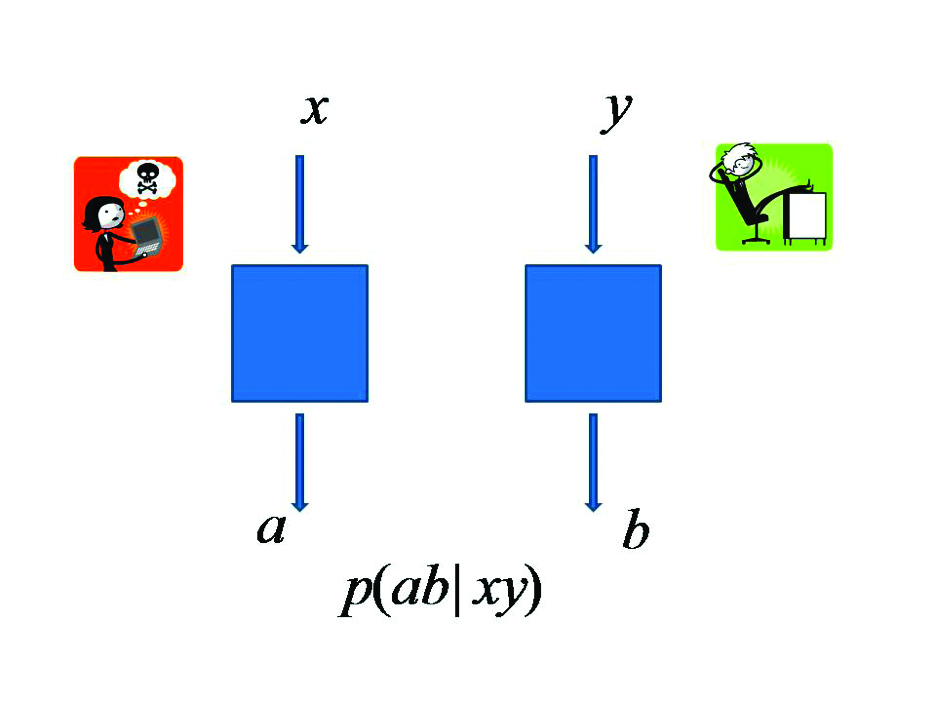
During his Center appointment Professor Junge will participate in a one-semester workshop on quantum information theory at the Mittag-Leffler Institute, Royal Swedish Academy of Sciences. He hopes to discover more interesting connections between quantum information theory and operator space theory. A particular focus will be quantum probabilities obtained by performing a number of different quantum experiments (x, y) with different outcomes (a, b) by different persons (Alice, Bob).
